 Widok zawartości stron
Widok zawartości stron
Zadziwiający ciąg liczb Fibonacciego
Co ma wspólnego średniowieczny włoski matematyk z prawidłowościami spotykanymi w przyrodzie? Okazuje się, że całkiem sporo.
Na wstępie przypomnijmy, że Ciąg Fibonacciego to ciąg liczb z których każda następna jest sumą dwóch poprzednich. Przedstawia się to następująco: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 itd. Rozejrzyjmy się teraz wokół nas. Na początek zwróćmy uwagę na ilość płatków czy liści: czermień błotna – 1 płatek, szczawik zajęczy – 3 listki i 5 płatków, dzika róża – 5 płatków, jesion – 13 listków, wężymord – 21 płatków. Takich prawidłowości można znaleźć wiele, choć oczywiście zdarzają się odstępstwa, ot chociażby czterolistna koniczyna.




Okazuje się, że ciąg liczb Fibonacciego posiada szereg ciekawych właściwości i tak: jeśli podzielimy dwie sąsiadujące ze sobą liczby, to otrzymamy w przybliżeniu wartość 1,618 a im większe liczby, tym dokładniejszy wynik. Sama liczba ilorazu nazywana jest złotą. Niekiedy nazywana jest też boską proporcją lub złotym podziałem. Na bazie tych liczb kreśli się tzw. złotą spiralę, uznawaną za graficzny obraz ciągu liczb Fibonacciego. Powstaje ona poprzez wpisanie w miejscach styczności kwadratów o bokach równych kolejnym liczbom ciągu.
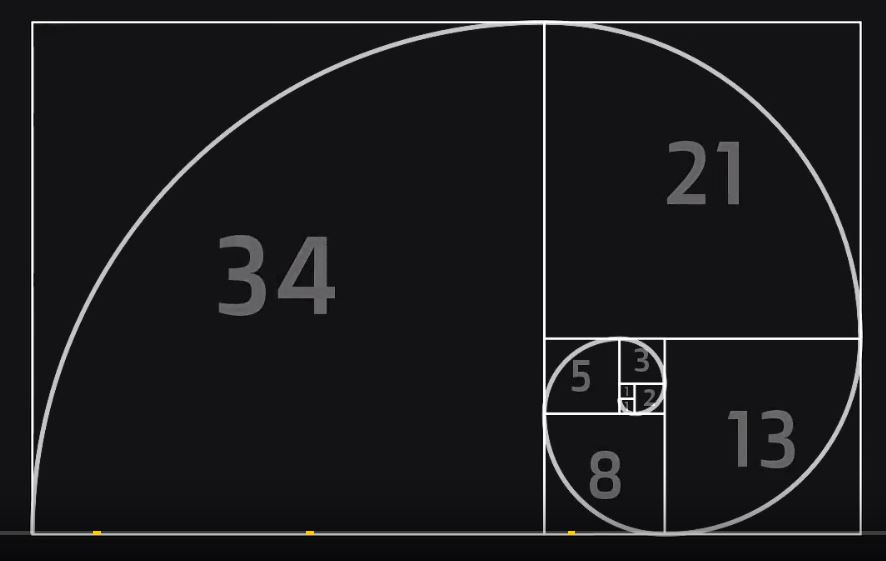
Odszukajmy odzwierciedlenie złotej spirali w przyrodzie. Znajdziemy ją bez trudu nie tylko w muszlach ślimaków, ale też w kwiatach słonecznika, szyszkach, stokrotkach czy ananasach. Co więcej, ilość spirali lewo- i prawoskrętnych to zwykle liczby ciągu Fibonacciego.

Układ liści na pędach podlega tym samym regułom. Dlaczego rośliny tak bardzo upodobały sobie liczby Fibonacciego i wynikające z nich zasady? Otóż okazuje się, że taki wzrost i rozwój pozwalają jak najlepiej wykorzystać światło docierające do rośliny.

Huragany, galaktyki spiralne – wszystkie one formują się zgodnie ze złotą spiralą. Takich przykładów można by podać wiele. Zadziwiającą ilość złotych proporcji znajdziemy również w... budowie ludzkiego ciała, ale to już zagadnienie z innej dziedziny.


